Transformasi wavelet adalah teknik matematika yang digunakan untuk menganalisis dan merepresentasikan data dalam domain frekuensi dan waktu secara bersamaan. Berikut adalah beberapa poin penting tentang transformasi wavelet:

• Wavelet: Wavelet adalah fungsi matematika yang digunakan dalam transformasi wavelet. Fungsi ini memiliki sifat lokal dan dapat merepresentasikan perubahan dalam waktu dan frekuensi. Beberapa jenis wavelet yang umum digunakan termasuk Haar, Daubechies, Symlets, dan Coiflets.
• Multi-resolusi: Transformasi wavelet memungkinkan analisis data dalam berbagai resolusi. Dengan menggunakan skala yang berbeda, transformasi wavelet dapat mengungkapkan detail halus dan kasar dalam data.
• Dekomposisi: Transformasi wavelet dapat memecah data menjadi komponen frekuensi yang berbeda. Proses ini melibatkan dekomposisi data menjadi aproksimasi (komponen rendah frekuensi) dan detail (komponen tinggi frekuensi) menggunakan filter wavelet.
• Rekonstruksi: Rekonstruksi adalah proses menggabungkan komponen frekuensi yang telah dipecah menjadi bentuk aslinya menggunakan filter wavelet yang berlawanan.
• Aplikasi: Transformasi wavelet memiliki berbagai aplikasi dalam pengolahan sinyal dan citra, termasuk kompresi citra, pengenalan pola, denoising, deteksi tepi, dan analisis data time series.

Transformasi wavelet digunakan dalam kompresi citra digital untuk mengurangi redundansi dan menghilangkan informasi yang tidak signifikan. Dengan menggunakan transformasi wavelet, citra dapat direpresentasikan dengan lebih efisien dalam domain frekuensi dan waktu.

Kompresi citra digital menggunakan transformasi wavelet adalah teknik yang digunakan untuk mereduksi ukuran data pada citra dengan tujuan untuk menghemat kapasitas penyimpanan data, mempercepat waktu transmisi data, dan mempercepat waktu komputasi saat pengolahan citra dilakukan. Berikut adalah langkah-langkah umum untuk melakukan kompresi citra digital menggunakan transformasi wavelet:

1. Membaca dan menampilkan file citra asli.
2. Melakukan transformasi wavelet diskrit (DWT) pada citra menggunakan jenis wavelet tertentu seperti Haar, Daubechies, Symlets, atau Coiflets.
3. Menghitung koefisien wavelet dan menghapus koefisien yang kecil untuk mengurangi ukuran data.
4. Melakukan rekonstruksi citra dari koefisien wavelet yang telah diubah.
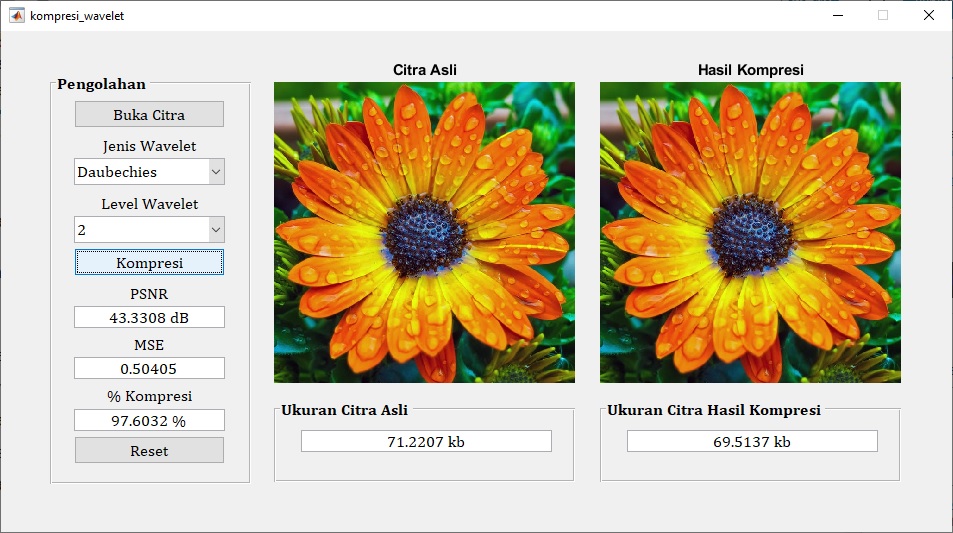
5. Menampilkan citra hasil kompresi.

Metode kompresi citra menggunakan transformasi wavelet dapat dilakukan dengan menggunakan berbagai perangkat lunak seperti MATLAB. Teknik ini dapat digunakan untuk berbagai jenis citra, termasuk citra berwarna. Metode ini dapat digunakan untuk melakukan kompresi citra secara lossless atau lossy, tergantung pada kebutuhan aplikasi.

Dalam era digital saat ini, gambar dan citra digital menjadi bagian integral dari berbagai aspek kehidupan kita. Namun, pengolahan, penyimpanan, dan transmisi citra digital memerlukan ruang dan sumber daya yang signifikan. Dalam artikel ini, kita akan menjelajahi bagaimana pemrograman menggunakan MATLAB dapat digunakan untuk melakukan kompresi citra digital dengan memanfaatkan Transformasi Wavelet, sebuah pendekatan yang kuat dalam mengurangi ukuran file citra tanpa mengorbankan kualitas visual.

1. Pendahuluan

Kompresi citra adalah proses mengurangi ukuran data citra untuk menghemat ruang penyimpanan dan mempercepat transmisi melalui jaringan. Transformasi Wavelet adalah salah satu teknik kompresi yang telah terbukti efektif dalam mengatasi tantangan kompresi citra, seperti mempertahankan detail penting sambil mengurangi redundansi.

2. Transformasi Wavelet: Konsep Dasar

Transformasi Wavelet melibatkan penguraian citra menjadi serangkaian gelombang atau wavelet yang merepresentasikan informasi dalam berbagai tingkat resolusi dan frekuensi. Dalam konteks pemrograman MATLAB, langkah-langkah berikut ini umumnya diikuti:

a. Pra-pemrosesan Citra

• Citra digital dimuat dan dapat dikenai pra-pemrosesan, seperti normalisasi kontras atau penyesuaian gamma.

b. Transformasi Wavelet

• Menggunakan fungsi seperti wavedec dalam MATLAB, citra diubah menjadi koefisien wavelet dalam berbagai tingkat.

c. Pengambilan Koefisien yang Signifikan

• Koefisien wavelet dengan amplitudo rendah, yang mewakili frekuensi tinggi, sering kali dapat diabaikan untuk kompresi.

d. Kuantisasi dan Pengkodean

• Koefisien yang dipertahankan dikuantisasi, yaitu nilai-nilai mereka dibulatkan ke level yang lebih rendah.
• Koefisien yang dikuantisasi kemudian dikodekan menggunakan algoritma kompresi seperti Huffman atau Run-Length Encoding (RLE).

3. Keuntungan Transformasi Wavelet dalam Kompresi

• Pertahankan Detail Penting: Transformasi Wavelet memungkinkan kompresi sambil mempertahankan detail penting, terutama di daerah-daerah penting citra.
• Pengaturan Kualitas: Dengan mengatur tingkat kuantisasi, kita dapat mengendalikan trade-off antara ukuran file dan kualitas visual.
• Adaptasi Terhadap Citra: Transformasi Wavelet dapat menyesuaikan diri dengan karakteristik citra, menghasilkan kompresi yang lebih efisien.

4. Implementasi Praktis dalam MATLAB

Penggunaan MATLAB untuk kompresi citra dengan Transformasi Wavelet melibatkan penggunaan fungsi-fungsi bawaan seperti wavedec, quantize, dan algoritma kompresi yang ada dalam toolbox MATLAB.

5. Kesimpulan

Pemrograman MATLAB memberikan kerangka yang kuat untuk eksplorasi dan implementasi Transformasi Wavelet dalam kompresi citra digital. Dalam dunia di mana kecepatan transmisi data dan efisiensi penyimpanan menjadi penting, teknik ini memberikan solusi yang dapat diandalkan untuk menjaga kualitas citra sambil mengurangi ukurannya. Dengan memahami konsep Transformasi Wavelet dan memanfaatkan alat-alat yang disediakan oleh MATLAB, kita dapat mengatasi tantangan kompresi citra digital secara efektif.

Source code beserta data lengkap pemrograman matlab di atas dapat diperoleh melalui halaman berikut ini: Source Code