Blog Archives
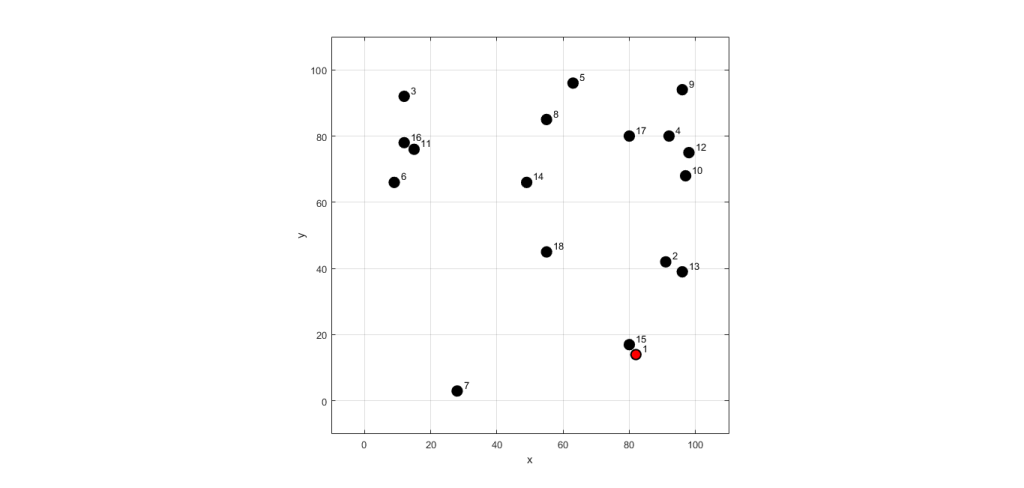
Perbandingan Algoritma Genetika, Partikel Swarm Optimization, dan Tabu Search dalam Menyelesaikan Travelling Salesman Problem
Travelling Salesman Problem (TSP) adalah salah satu permasalahan optimasi kombinatorial yang telah menantang para peneliti selama beberapa dekade. TSP melibatkan pencarian jalur terpendek yang melalui setiap titik (kota) tepat satu kali dan kembali ke titik awal. Algoritma optimasi yang populer digunakan untuk menyelesaikan TSP antara lain adalah Algoritma Genetika, Partikel Swarm Optimization (PSO), dan Tabu Search. Dalam artikel ini, kita akan mendalami tentang ketiga algoritma ini dan membandingkannya dalam konteks penyelesaian Travelling Salesman Problem.
-read more->Kompresi Citra dengan Metode Discrete Cosine Transform (DCT)
Discrete Cosine Transform (DCT) adalah teknik transformasi matematika yang digunakan untuk mengurangi redundansi dalam citra digital dan digunakan dalam kompresi citra. Berikut adalah langkah-langkah umum untuk melakukan kompresi citra menggunakan DCT:
- Membaca citra: Citra asli dibaca dan dipecah menjadi blok-blok kecil.
- Transformasi DCT: Setiap blok citra diubah menjadi domain frekuensi menggunakan transformasi DCT. DCT menghasilkan koefisien frekuensi yang merepresentasikan informasi dalam citra.
- Kuantisasi: Koefisien frekuensi yang dihasilkan oleh DCT dikuantisasi untuk mengurangi jumlah bit yang digunakan untuk merepresentasikan citra. Kuantisasi menghilangkan informasi yang tidak signifikan dalam citra.
- Kompresi: Kuantisasi menghasilkan koefisien frekuensi yang lebih kecil. Koefisien frekuensi yang kecil ini dihapus atau diubah menjadi nol untuk mengurangi ukuran data.
- Rekonstruksi: Citra dikembalikan ke domain spasial dari domain frekuensi menggunakan transformasi invers DCT.
Kompresi Citra Digital Menggunakan Transformasi Wavelet
Transformasi wavelet adalah teknik matematika yang digunakan untuk menganalisis dan merepresentasikan data dalam domain frekuensi dan waktu secara bersamaan. Berikut adalah beberapa poin penting tentang transformasi wavelet:
- Wavelet: Wavelet adalah fungsi matematika yang digunakan dalam transformasi wavelet. Fungsi ini memiliki sifat lokal dan dapat merepresentasikan perubahan dalam waktu dan frekuensi. Beberapa jenis wavelet yang umum digunakan termasuk Haar, Daubechies, Symlets, dan Coiflets.
- Multi-resolusi: Transformasi wavelet memungkinkan analisis data dalam berbagai resolusi. Dengan menggunakan skala yang berbeda, transformasi wavelet dapat mengungkapkan detail halus dan kasar dalam data.
- Dekomposisi: Transformasi wavelet dapat memecah data menjadi komponen frekuensi yang berbeda. Proses ini melibatkan dekomposisi data menjadi aproksimasi (komponen rendah frekuensi) dan detail (komponen tinggi frekuensi) menggunakan filter wavelet.
- Rekonstruksi: Rekonstruksi adalah proses menggabungkan komponen frekuensi yang telah dipecah menjadi bentuk aslinya menggunakan filter wavelet yang berlawanan.
- Aplikasi: Transformasi wavelet memiliki berbagai aplikasi dalam pengolahan sinyal dan citra, termasuk kompresi citra, pengenalan pola, denoising, deteksi tepi, dan analisis data time series.
Penerapan Logika Fuzzy untuk Sistem Pengatur Kecepatan Mesin dengan Sensor Suhu dan Sensor Cahaya
Dalam dunia teknologi modern, sistem otomasi menjadi semakin penting dalam mengontrol berbagai proses dan perangkat. Salah satu pendekatan yang populer dalam pengendalian sistem adalah menggunakan logika fuzzy. Dalam artikel ini, kami akan menjelaskan penerapan logika fuzzy untuk mengatur kecepatan mesin berdasarkan data dari sensor suhu dan sensor cahaya. Kami akan membahas bagaimana logika fuzzy dapat membantu mengambil keputusan berdasarkan masukan dari kedua sensor tersebut, serta bagaimana implementasinya dilakukan menggunakan perangkat lunak MATLAB.
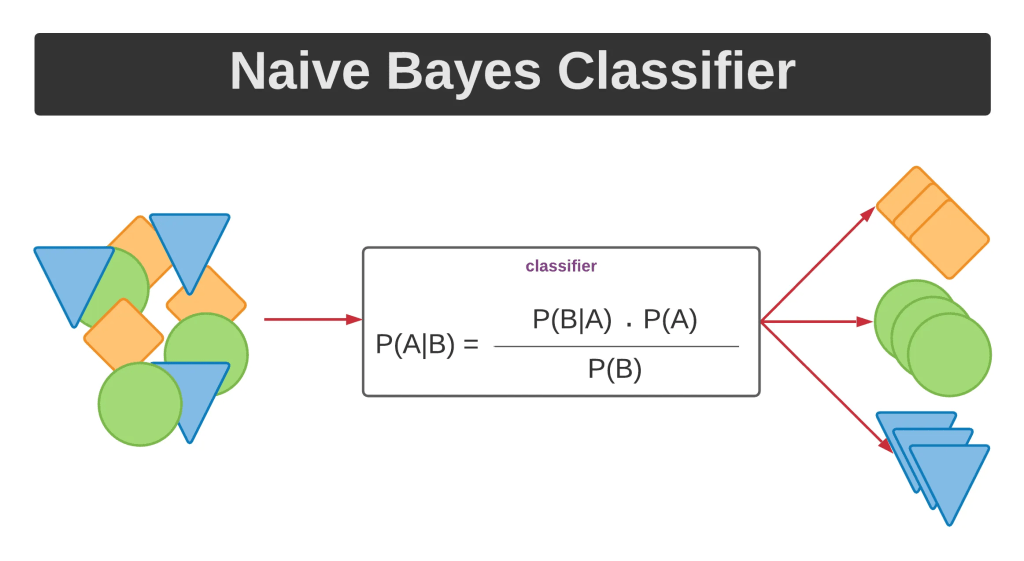
-read more->Memahami Algoritma Naive Bayes: Konsep dan Penerapan
Algoritma Naive Bayes adalah pendekatan klasifikasi yang populer dalam dunia kecerdasan buatan dan pemrosesan bahasa alami. Artikel ini akan menjelaskan konsep dasar algoritma Naive Bayes, mengapa algoritma ini penting, serta bagaimana mengimplementasikannya dalam berbagai aplikasi.
Algoritma Naive Bayes didasarkan pada teorema probabilitas Bayes dan digunakan untuk mengklasifikasikan data ke dalam kategori yang sesuai. Meskipun memiliki asumsi “naif” (sederhana) tentang independensi fitur, algoritma ini sering memberikan hasil yang memuaskan dalam berbagai konteks. Naive Bayes telah sukses diterapkan dalam spam filtering, analisis sentimen, klasifikasi dokumen, dan banyak aplikasi lainnya.
-read more->