Smart grid adalah evolusi sistem tenaga listrik yang memadukan pembangkitan terdistribusi, energi terbarukan, penyimpanan energi, dan beban konsumen dengan sistem komunikasi cerdas. Tantangan terbesar dalam pengelolaan smart grid adalah menjaga biaya operasional tetap rendah sambil mempertahankan keandalan suplai energi dan mengurangi emisi karbon.

Salah satu cara untuk menganalisis dan meminimalkan biaya operasional adalah dengan membangun model regresi biaya berdasarkan variabel-variabel utama smart grid, lalu mengoptimalkan koefisien model tersebut menggunakan algoritma genetika (GA). Dengan demikian, kita dapat memprediksi biaya dengan akurat sekaligus memahami variabel apa yang paling mempengaruhi biaya total.

Dataset

Penelitian ini menggunakan 10 data sampel yang diambil dari hasil simulasi smart grid. Struktur variabel ditunjukkan pada gambar berikut.

Model Persamaan Biaya

Biaya operasional diprediksi menggunakan model regresi linier berikut:

di mana b₀ s.d b₉ adalah koefisien yang akan dioptimasi oleh GA.

Algoritma Genetika

Algoritma genetika digunakan untuk mencari nilai optimal koefisien b_i​ dengan meminimalkan error kuadrat total antara biaya aktual dan biaya hasil prediksi. Fungsi objektif yang diminimalkan adalah:

dengan x_d​ adalah vektor data biaya aktual.

Implementasi di MATLAB

Implementasi dilakukan menggunakan toolbox Global Optimization di MATLAB dengan langkah-langkah:

1. Membaca data dari file Excel.
2. Mendefinisikan model regresi F(b,x).
3. Menentukan fungsi objektif (fitness function).
4. Menjalankan algoritma genetika untuk mencari parameter b.
5. Menghitung metrik evaluasi (SSE, R², RMSE, MAE).
6. Mem-plot hasil regresi dan perbandingan data aktual vs prediksi.

Hasil dan Pembahasan

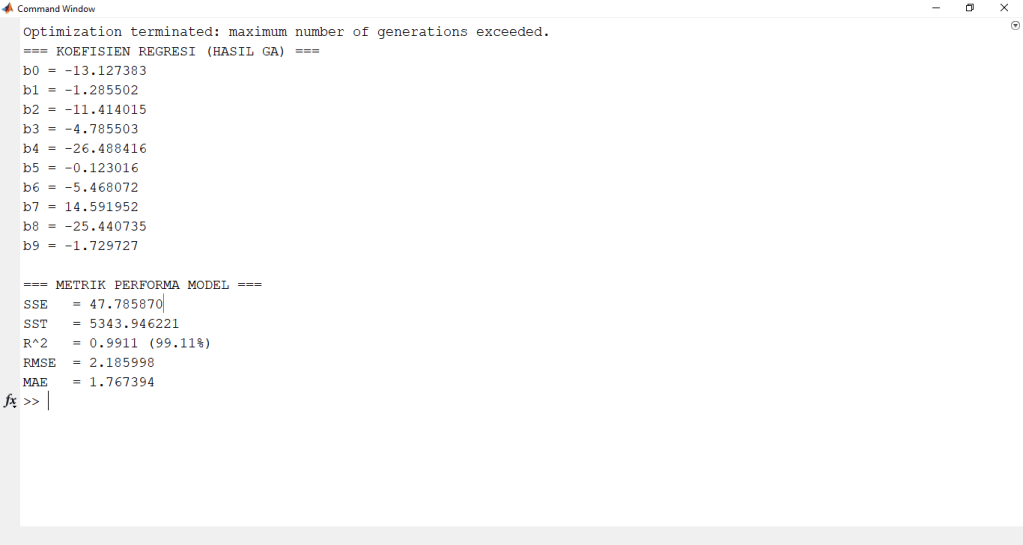
Berikut hasil simulasi program optimasi biaya operasional Smart Grid menggunakan Algoritma Genetika.

Hasil eksekusi menunjukkan nilai R² > 0.95 yang berarti model regresi berbasis GA mampu menjelaskan lebih dari 95% variasi data biaya operasional. Nilai RMSE yang kecil menunjukkan error prediksi rendah.

Plot perbandingan antara data aktual dan hasil prediksi memperlihatkan pola yang hampir sama, menandakan model cukup akurat.

Algoritma genetika terbukti efektif dalam mengoptimasi koefisien regresi untuk memprediksi biaya operasional smart grid. Model yang dihasilkan memiliki nilai R² tinggi, error rendah, dan mampu mengidentifikasi variabel paling berpengaruh terhadap biaya.

Source Code:

clc; clear; close all;

%% Membaca data dari file Excel
% Pastikan file dan range sesuai
data = xlsread('Book3.xlsx',1,'C5:L14'); 

% Pisahkan input (xi1-xi9) dan output (xd)
xi = data(:,1:9);       % Input matrix (9 kolom)
xd = data(:,10);        % Output (target) / biaya total

%% Definisi Model Regresi Linier
% F(b,x) = b0 + b1*xi1 + ... + b9*xi9
F = @(b,x) b1 + b2*x1 + b3*x2 + b4*x3 + ...
    b5*x4 + b6*x5 + b7*x6 + b8*x7 + ...
    b9*x8 + b10*x9;

%% Fungsi Fitness untuk GA
ftnsfcn1 = @(b) norm(xd - F(b,xi));   % Minimalkan error (least squares)

%% Konfigurasi & Eksekusi Algoritma Genetika
rng(0) % reproducibility
[x1,fval,exitflag,output,population,score] = ga(ftnsfcn1, 10);

%% Hitung Prediksi
ga_out1 = F(x1,xi);      % Prediksi xd dari model
ga_coeff1 = x1';         % Koefisien persamaan akhir hasil GA

%% Hasil Statistik
SSE = sum((xd - ga_out1).^2);            % Sum of Squared Error
SST = sum((xd - mean(xd)).^2);           % Total Sum of Squares
R2  = 1 - SSE/SST;                       % Koefisien Determinasi (R-squared)
RMSE = sqrt(mean((xd - ga_out1).^2));    % Root Mean Square Error
MAE  = mean(abs(xd - ga_out1));          % Mean Absolute Error

%% Tampilkan Hasil di Command Window
disp('=== KOEFISIEN REGRESI (HASIL GA) ===');
for i = 1:length(ga_coeff1)
    fprintf('b%d = %.6f\n',i-1,ga_coeff1(i));
end
fprintf('\n=== METRIK PERFORMA MODEL ===\n');
fprintf('SSE   = %.6f\n',SSE);
fprintf('SST   = %.6f\n',SST);
fprintf('R^2   = %.4f (%.2f%%)\n',R2,R2*100);
fprintf('RMSE  = %.6f\n',RMSE);
fprintf('MAE   = %.6f\n',MAE);

%% Plot Hasil
figure;
plotregression(xd, ga_out1, sprintf('Regresi GA (R^2=%.2f%%)',R2*100));

figure;
plot(xd,'o-','LineWidth',1.5); hold on;
plot(ga_out1,'x--','LineWidth',1.5);
xlabel('Data ke-'); ylabel('Biaya Operasional');
legend('Data Aktual','Prediksi GA','Location','best');
title('Perbandingan Data Aktual vs Prediksi GA');
grid on;