Jaringan Syaraf Tiruan Radial Basis Function untuk Memprediksi Jumlah Penduduk
Memprediksi jumlah penduduk suatu daerah merupakan tugas penting dalam perencanaan perkotaan, perencanaan sumber daya, dan pengambilan keputusan pemerintah. Metode tradisional seperti regresi linier sering digunakan untuk tujuan ini, tetapi kadang-kadang metode yang lebih kompleks diperlukan untuk mengatasi data yang rumit. Salah satu pendekatan yang muncul adalah menggunakan Jaringan Syaraf Tiruan Radial Basis Function (RBF-NN) untuk memprediksi jumlah penduduk. Dalam artikel ini akan dijelaskan konsep dasar RBF-NN dan bagaimana ia dapat digunakan dalam konteks ini.
Apa itu Jaringan Syaraf Tiruan Radial Basis Function (RBF-NN)?
Jaringan Syaraf Tiruan Radial Basis Function (RBF-NN) adalah salah satu jenis jaringan syaraf tiruan yang memiliki tiga lapisan utama: lapisan input, lapisan tersembunyi (hidden layer) dengan fungsi basis radial, dan lapisan output. RBF-NN memiliki kemampuan untuk memodelkan hubungan nonlinier yang kompleks antara masukan dan keluaran. Ini terutama berguna ketika data memiliki pola yang sulit diidentifikasi oleh metode linier.
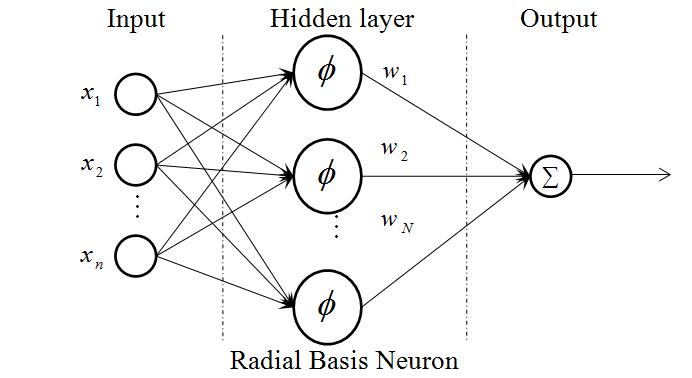
Bagian kunci dari RBF-NN adalah lapisan tersembunyi dengan fungsi basis radial. Fungsi basis radial adalah fungsi matematis yang menghasilkan respons tinggi ketika masukan berada dalam jarak tertentu dari pusat tertentu, dan respons rendah ketika masukan berada jauh dari pusat tersebut. Hal ini memungkinkan jaringan untuk mengidentifikasi pola dalam data yang terkait dengan lokasi tertentu.
Menerapkan RBF-NN untuk Prediksi Jumlah Penduduk
Bagaimana kita dapat menggunakan RBF-NN untuk memprediksi jumlah penduduk suatu daerah? Berikut adalah langkah-langkah umum yang dapat diambil:
1. Pengumpulan Data
Pertama-tama, kita perlu mengumpulkan data historis tentang jumlah penduduk daerah tersebut selama beberapa tahun terakhir. Data ini harus mencakup berbagai faktor seperti pertumbuhan ekonomi, imigrasi, tingkat kelahiran, tingkat kematian, dan faktor-faktor lain yang memengaruhi jumlah penduduk.
2. Preprocessing Data
Data kemudian perlu diproses dan disiapkan untuk digunakan dalam jaringan RBF-NN. Ini mungkin termasuk normalisasi data, penghapusan outlier, dan pemilihan fitur yang relevan.
3. Pembentukan Jaringan
Selanjutnya, kita harus membentuk jaringan RBF-NN. Ini melibatkan penentuan jumlah neuron dalam lapisan tersembunyi, pemilihan fungsi basis radial, dan inisialisasi parameter jaringan.
4. Pelatihan Jaringan
Data yang telah diproses digunakan untuk melatih jaringan RBF-NN. Selama pelatihan, jaringan akan mempelajari hubungan antara masukan (faktor-faktor yang memengaruhi jumlah penduduk) dan keluaran (jumlah penduduk aktual).
5. Validasi dan Evaluasi
Setelah pelatihan, kita perlu memvalidasi kinerja jaringan dengan menggunakan data uji yang tidak digunakan dalam pelatihan. Kinerja jaringan dapat diukur dengan berbagai metrik seperti Mean Absolute Error (MAE) atau Root Mean Square Error (RMSE).
6. Prediksi Jumlah Penduduk
Setelah jaringan dilatih dan divalidasi dengan baik, kita dapat menggunakannya untuk melakukan prediksi jumlah penduduk berdasarkan faktor-faktor yang diberikan.
Manfaat Penggunaan RBF-NN dalam Prediksi Jumlah Penduduk
Mengapa kita harus memilih RBF-NN dalam konteks ini? Berikut adalah beberapa manfaat penggunaannya:
- Kemampuan Nonlinier: RBF-NN mampu menangkap hubungan nonlinier antara faktor-faktor yang memengaruhi jumlah penduduk. Ini lebih fleksibel dibandingkan dengan model linier.
- Generalisasi: RBF-NN dapat mempelajari pola dari data historis dan menerapkan pengetahuannya untuk memprediksi masa depan dengan baik.
- Fleksibilitas: Jumlah neuron dalam lapisan tersembunyi dapat disesuaikan untuk mengatur kompleksitas model. Ini memungkinkan penyesuaian yang lebih baik dengan data yang ada.
- Kemampuan Manajemen Data Noisy: RBF-NN dapat mengatasi data yang noisy atau data yang tidak lengkap dengan baik, asalkan dilatih dengan benar.
- Interpretasi: Anda dapat memahami bagaimana jaringan membuat prediksi dengan memeriksa bobot dan pusat fungsi basis radial.
Meskipun RBF-NN memiliki manfaat yang signifikan dalam pemodelan jumlah penduduk, penting untuk diingat bahwa keberhasilan prediksi bergantung pada kualitas data dan perancangan yang baik dari jaringan. Dengan pendekatan yang tepat, RBF-NN dapat menjadi alat yang kuat dalam perencanaan dan pengambilan keputusan yang berkaitan dengan pertumbuhan populasi.
Jaringan Syaraf Tiruan Radial Basis Function (RBF-NN) adalah alat yang kuat dalam memprediksi jumlah penduduk suatu daerah dengan kemampuan untuk menangkap hubungan nonlinier antara faktor-faktor yang memengaruhi jumlah penduduk. Dengan pengumpulan data yang baik, preprocessing yang tepat, dan perancangan jaringan yang cermat, RBF-NN dapat menjadi alat yang berharga dalam perencanaan perkotaan, perencanaan sumber daya, dan pengambilan keputusan pemerintah untuk masa depan yang lebih baik.
Berikut ini merupakan contoh aplikasi pemrograman menggunakan bahasa pemrograman matlab untuk melakukan prediksi jumlah penduduk pada suatu daerah X dengan sistem prediksi urutan waktu menggunakan algoritma jaringan syaraf tiruan radial basis function (rbf neural network).
Langkah-langkah nya adalah sebagai berikut:
1. Mempersiapkan data jumlah penduduk. Data jumlah penduduk di suatu daerah X disajikan per bulan dari tahun 2006 sampai dengan tahun 2016.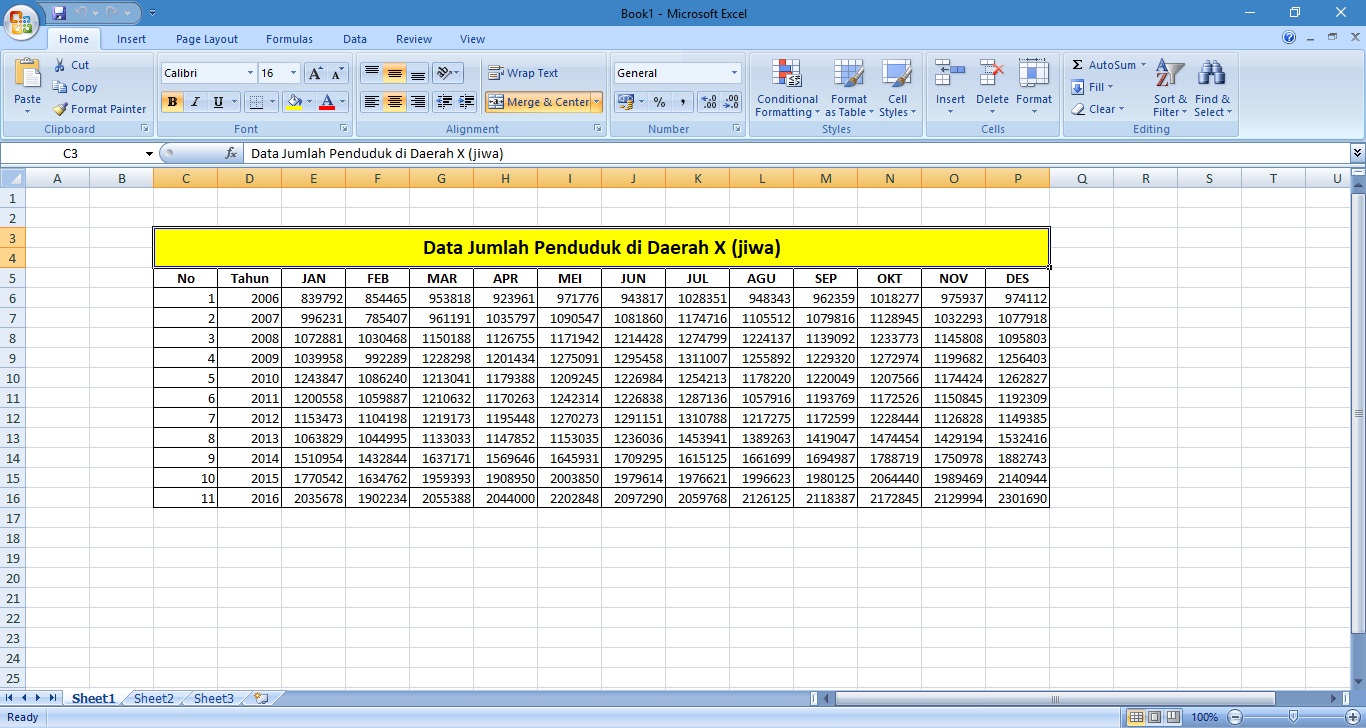
2. Untuk mereduksi perhitungan komputasi yang terlalu besar, maka dilakukan normalisasi data ke dalam range 0,1 s.d 0,9 menggunakan persamaan berikut:
di mana:
X’ = data hasil normalisasi
X = data asli/data awal
a = nilai maksimum data asli
b = nilai minimum data asli
Perintah yang digunakan yaitu:
clc; clear; close all; warning off all;
data = xlsread('Book1',1,'E6:P16');
% Proses Normalisasi Data
max_data = max(max(data));
min_data = min(min(data));
[m,n] = size(data);
data_norm = zeros(m,n);
for x = 1:m
for y = 1:n
data_norm(x,y) = 0.1+0.8*(data(x,y)-min_data)/(max_data-min_data);
end
end
sehingga diperoleh data hasil normalisasi seperti yang ditunjukkan pada gambar di bawah ini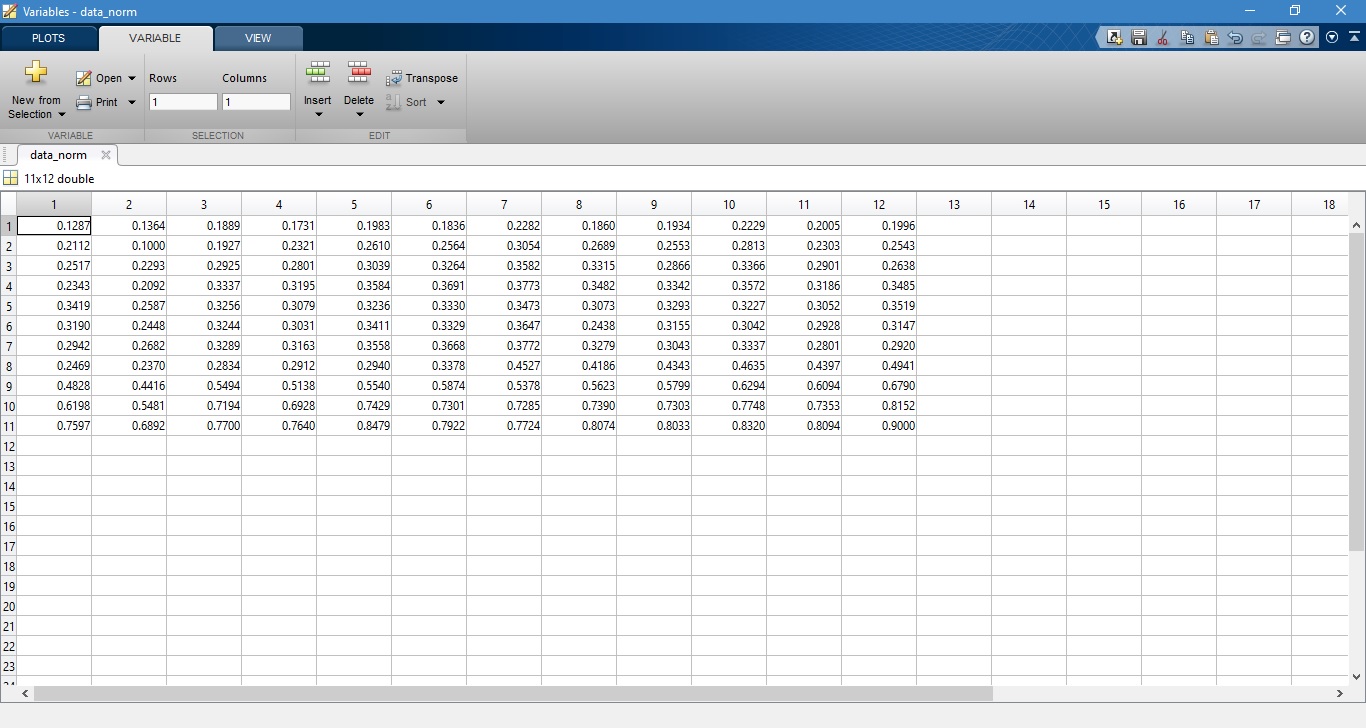
3. Pada pemrograman ini, data jumlah penduduk diprediksi berdasarkan data jumlah penduduk 12 bulan sebelumnya. Data latih yang digunakan adalah data jumlah penduduk dari bulan Januari 2006 sampai dengan bulan November 2012 (7 tahun). Sedangkan target latih adalah data jumlah penduduk dari bulan Januari 2007 sampai dengan bulan Desember 2012 (7 tahun). Gambaran dari penggunaan data latih dan target latih ditunjukkan pada tabel berikut: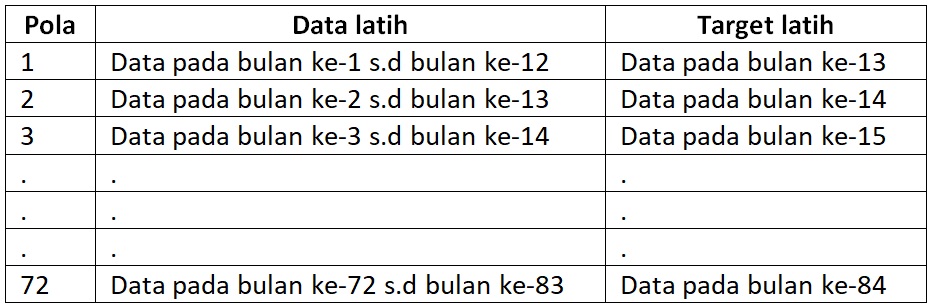
Perintah yang digunakan untuk menyusun data latih dan target latih seperti pada pola di atas adalah:
% Pelatihan
data_norm = data_norm';
tahun_latih = 7; % Januari 2006 s.d November 2012
data_latih = zeros(12,72);
jumlah_bulan = 12;
for n = 1:jumlah_bulan*(tahun_latih-1)
for m = 1:jumlah_bulan
data_latih(m,n) = data_norm(m+n-1);
end
end
target_latih = data_norm(jumlah_bulan+1:jumlah_bulan*tahun_latih); % Januari 2007 s.d Desember 2012
sehingga susunan data latih dan target latih yang diperoleh adalah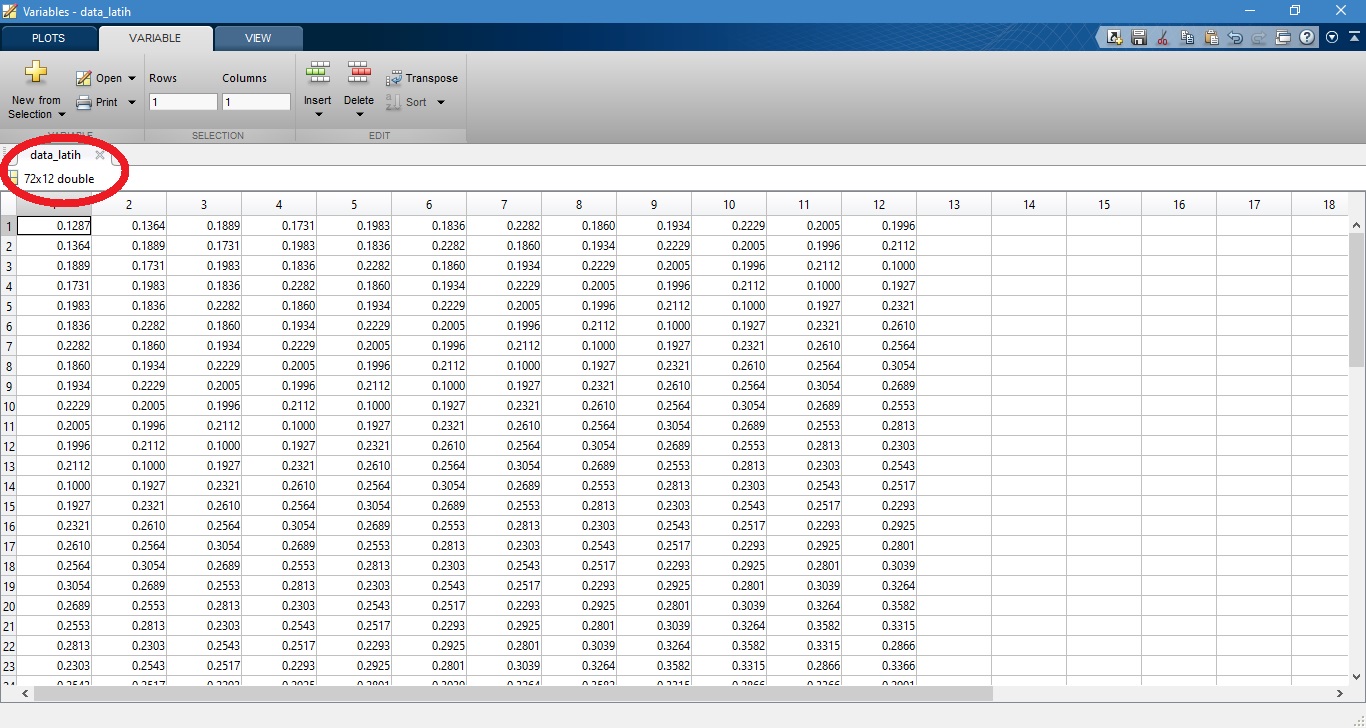
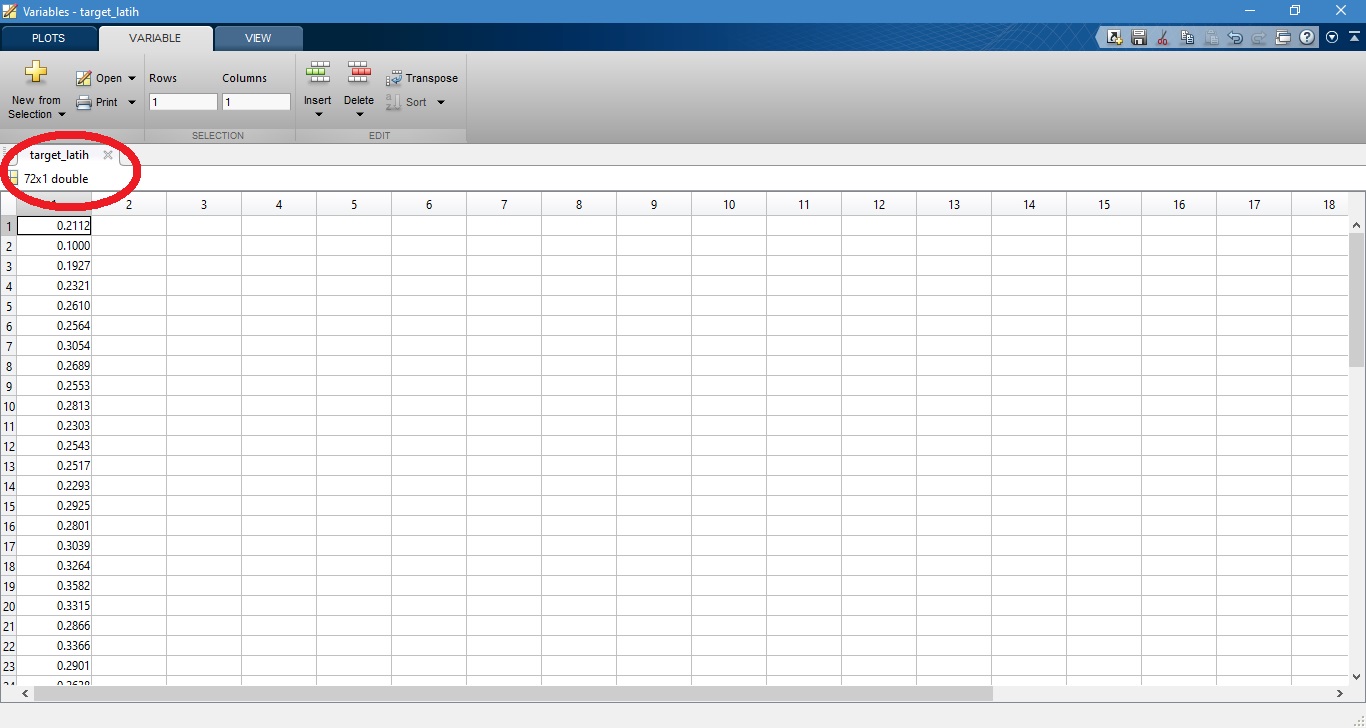
4. Melakukan pelatihan jaringan radial basis function dengan masukan berupa data latih dan target latih yang sebelumnya telah disusun.
Perintah yang digunakan adalah:
% performance goal (MSE)
error_goal = 1e-6;
% choose a spread constant
spread = 1.2;
% choose max number of neurons
K = 10;
% number of neurons to add between displays
Ki = 20;
% create a neural network
net = newrb(data_latih,target_latih,error_goal,spread,K,Ki);
% inisialisasi bobot
load bobot_awal
net.IW{1,1} = bobot_hidden;
net.LW{2,1} = bobot_keluaran;
net.b{1,1} = bias_hidden;
net.b{2,1} = bias_keluaran;
% Proses training
net.trainFcn = 'traingdx';
[net_keluaran,tr,~,E] = train(net,data_latih,target_latih);
% Hasil setelah pelatihan
nilai_error = E;
error_MSE = (1/n)*sum(nilai_error.^2);
save net_keluaran.mat net_keluaran
Tampilan pelatihan jaringan ditunjukkan pada gambar di bawah ini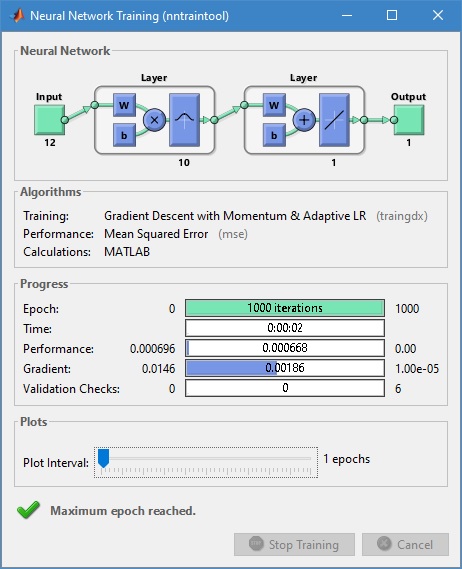
5. Menampilkan hasil pelatihan dalam bentuk grafik beserta nilai MSE (Mean Square Error) dan koefisien korelasi.
Perintah yang digunakan adalah:
% Hasil prediksi
hasil_latih = sim(net_keluaran,data_latih);
hasil_latih = ((hasil_latih-0.1)*(max_data-min_data)/0.8)+min_data;
data = data';
target_latih_asli = data(jumlah_bulan+1:jumlah_bulan*tahun_latih); % januari 2007 s.d januari 2013
% Menampilkan grafik hasil pelatihan
figure,
plot(hasil_latih,'bo-')
hold on
plot(target_latih_asli,'ro-')
hold off
grid on
title(strcat(['Grafik Keluaran JST vs Target dengan nilai MSE = ',...
num2str(error_MSE)]))
xlabel('Bulan ke-')
ylabel('Jumlah Penduduk')
legend('Keluaran JST','Target','Location','Best')
figure,
plotregression(target_latih_asli,hasil_latih,'Regression')
Grafik keluaran yang dihasilkan dari proses pelatihan adalah sebagai berikut: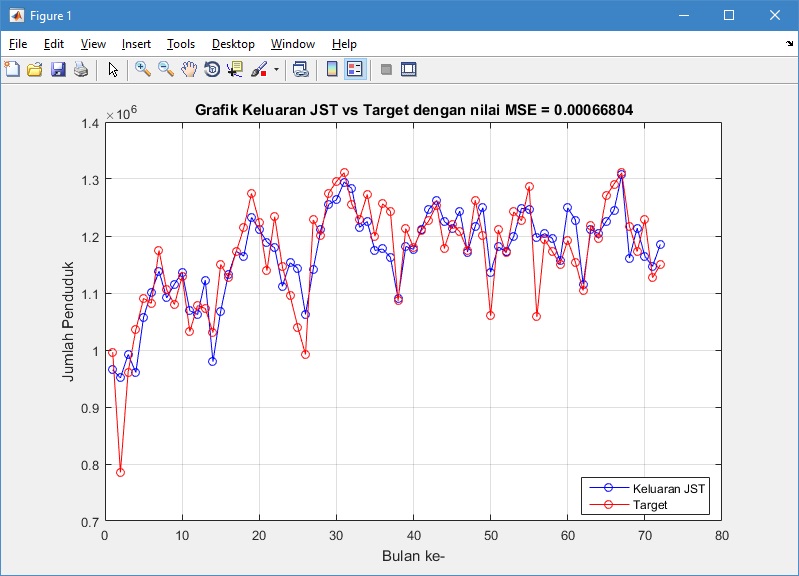
Sedangkan grafik korelasi yang diperoleh yaitu: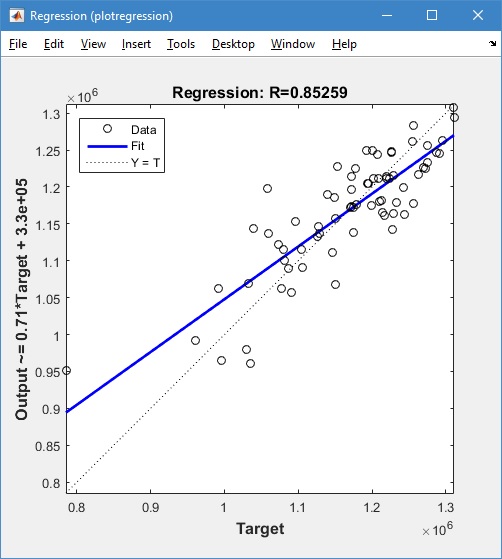
Nilai MSE dan koefisien korelasi yang dihasilkan pada proses pelatihan berturut-turut adalah sebesar 0.00066804 dan 0.85259. Kedua nilai tersebut menunjukkan bahwa proses pelatihan jaringan radial basis function dapat memprediksi jumlah penduduk dengan baik, sehingga jaringan yang diperoleh dapat digunakan untuk melakukan prediksi pada proses pengujian.
5. Mempersiapkan data uji dan target uji. Pada proses pengujian, target uji digunakan hanya untuk memvalidasi hasil pengujian. Gambaran penggunaan data uji dan target uji ditunjukkan pada tabel berikut: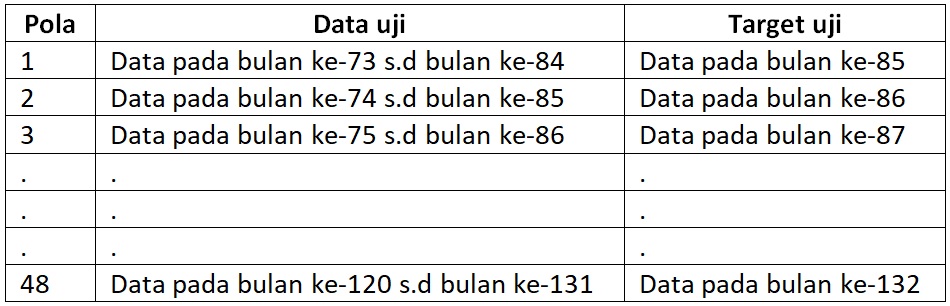
Perintah yang digunakan untuk menyusun data uji dan target uji seperti pada pola di atas adalah:
% Pengujian
tahun_uji = 5; % Desember 2012 s.d November 2016
data_uji = zeros(12,48);
jumlah_bulan = 12;
for n = 1:jumlah_bulan*(tahun_uji-1)
for m = 1:jumlah_bulan
data_uji(m,n) = data_norm(72+m+n-1);
end
end
target_uji = data_norm(jumlah_bulan*tahun_uji+1:(jumlah_bulan*tahun_uji)+48); % Januari 2013 s.d Desember 2016
sehingga susunan data uji dan target uji yang diperoleh adalah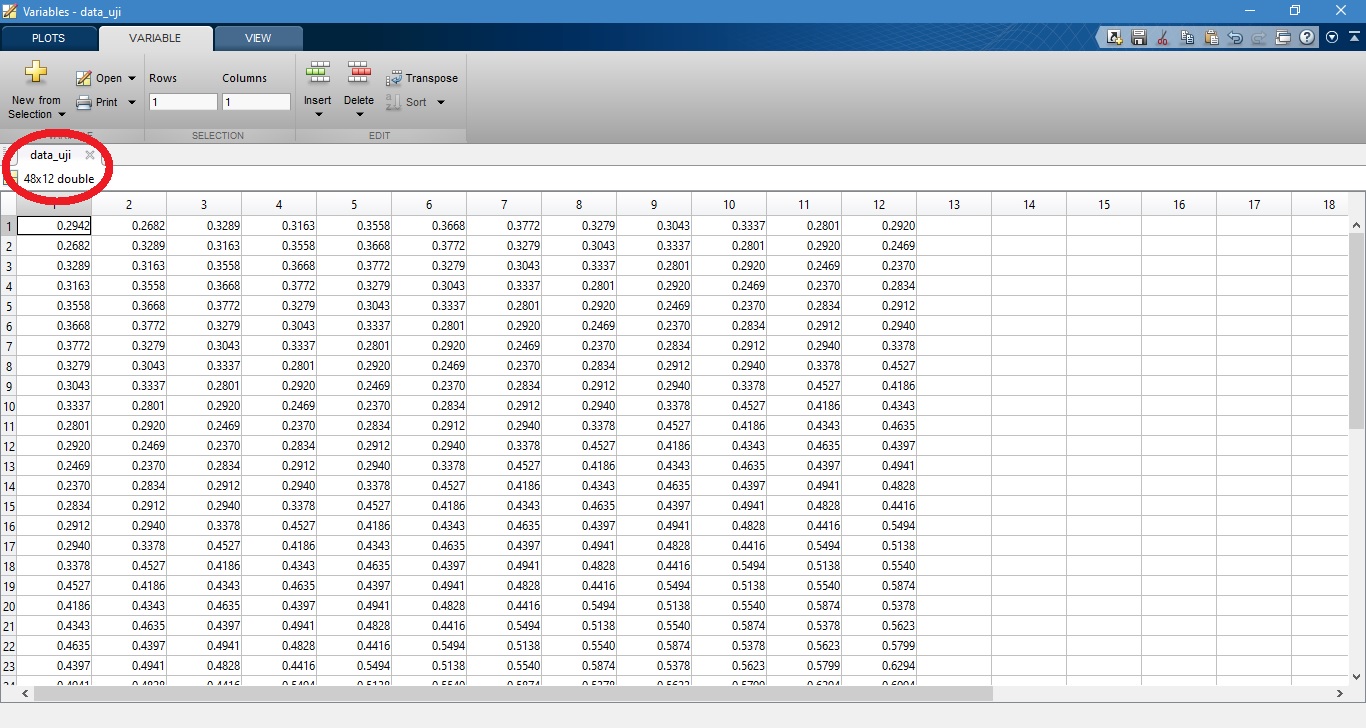
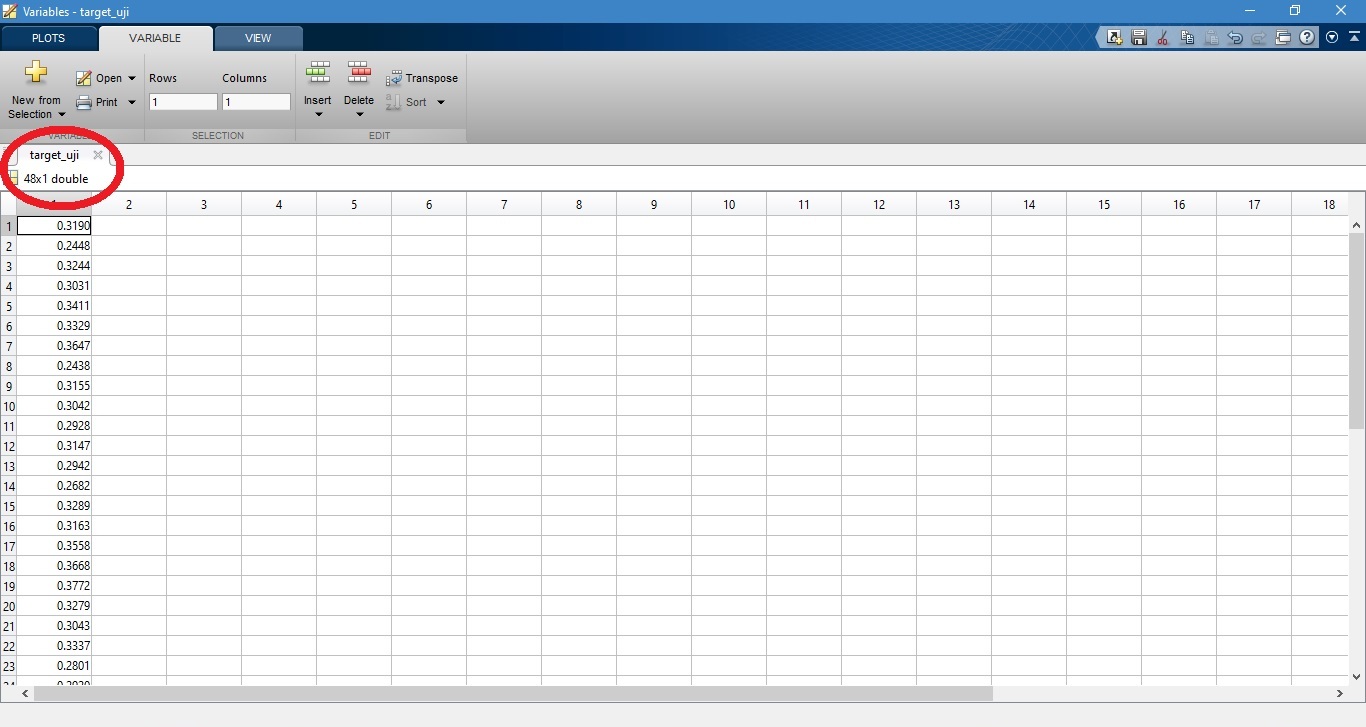
6. Menampilkan hasil pengujian dalam bentuk grafik beserta nilai MSE (Mean Square Error) dan koefisien korelasi.
Perintah yang digunakan adalah:
% Hasil prediksi
hasil_uji = sim(net_keluaran,data_uji);
error_MSE_uji = mse(target_uji,hasil_uji);
hasil_uji = ((hasil_uji-0.1)*(max_data-min_data)/0.8)+min_data;
target_uji_asli = data(jumlah_bulan*tahun_uji+1:(jumlah_bulan*tahun_uji)+48); % Januari 2013 s.d Desember 2016
% Menampilkan grafik hasil pengujian
figure,
plot(hasil_uji,'bo-')
hold on
plot(target_uji_asli,'ro-')
hold off
grid on
title(strcat(['Grafik Keluaran JST vs Target dengan nilai MSE = ',...
num2str(error_MSE_uji)]))
xlabel('Bulan ke-')
ylabel('Jumlah Penduduk')
legend('Keluaran JST','Target','Location','Best')
figure,
plotregression(target_uji_asli,hasil_uji,'Regression')
Grafik keluaran yang dihasilkan dari proses pengujian adalah sebagai berikut: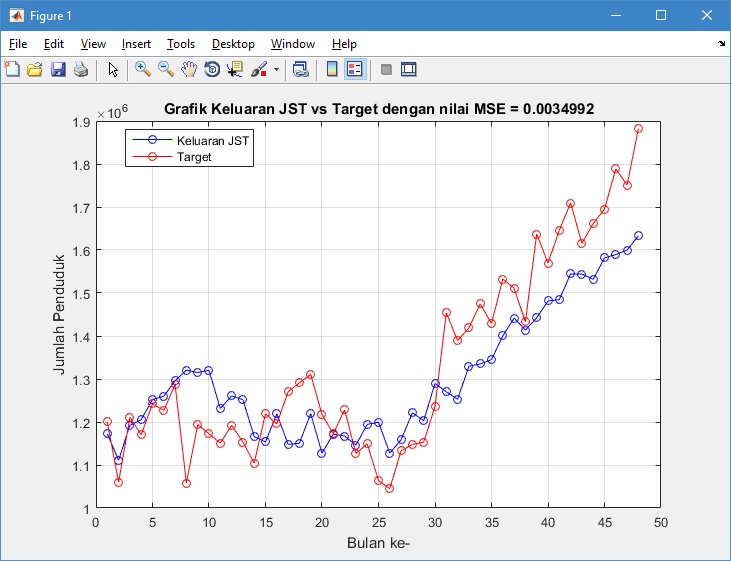
Sedangkan grafik korelasi yang diperoleh yaitu: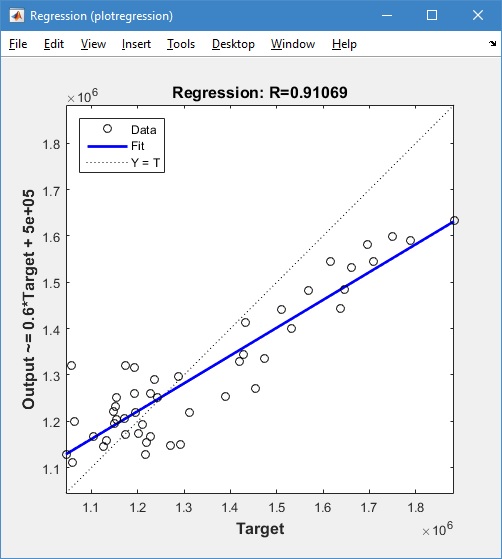
Nilai MSE dan koefisien korelasi yang dihasilkan pada proses pengujian berturut-turut adalah sebesar 0.0034992 dan 0.91069. Kedua nilai tersebut menunjukkan bahwa proses pengujian jaringan radial basis function dapat memprediksi jumlah penduduk dengan baik, sehingga jaringan yang diperoleh dapat digunakan untuk melakukan prediksi jumlah penduduk pada bulan-bulan berikutnya.
7. Melakuan prediksi untuk bulan Januari 2017 sampai dengan Desember 2017 (12 bulan).
Perintah yang digunakan adalah:
load net_keluaran
load data_prediksi_rbf
load hasil_prediksi_rbf
data_prediksi = data_prediksi_rbf(:,12);
% Hasil prediksi
hasil_prediksi_norm = sim(net_keluaran,data_prediksi);
hasil_prediksi = ((hasil_prediksi_norm-0.1)*(max_data-min_data)/0.8)+min_data;
data_prediksi = data_prediksi(2:end,:);
data_prediksi = [data_prediksi;hasil_prediksi_norm];
data_prediksi_rbf = [data_prediksi_rbf,data_prediksi];
hasil_prediksi_rbf = [hasil_prediksi_rbf,hasil_prediksi];
% save data_prediksi_rbf data_prediksi_rbf
% save hasil_prediksi_rbf hasil_prediksi_rbf
figure,
plot(hasil_prediksi_rbf);
grid on
title('Hasil Prediksi Jumlah Penduduk Bulan Januari 2017 s.d Desember 2017')
xlabel('Bulan ke-')
ylabel('Jumlah Penduduk')
legend('Hasil Prediksi','Target','Location','Best')
Grafik hasil prediksi yang dihasilkan yaitu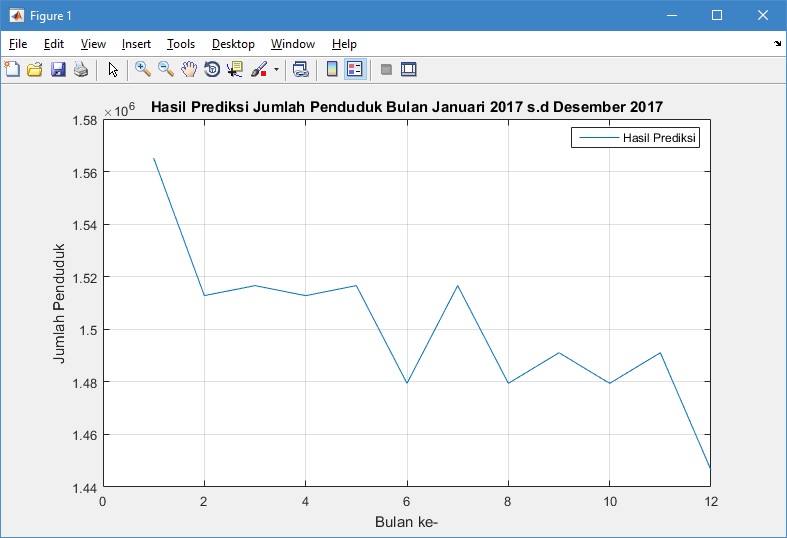
Hasil dari pelatihan, pengujian, dan prediksi di atas menunjukkan bahwa jaringan syaraf tiruan radial basis function mampu untuk melakukan prediksi jumlah penduduk dengan baik.
File source code lengkap beserta data pada pemrograman di atas dapat diperoleh melalui halaman berikut ini: Source Code
Posted on September 13, 2023, in Data mining and tagged algoritma dan pemrograman, algoritma jaringan syaraf tiruan, analisis data, jaringan syaraf tiruan, Jaringan Syaraf Tiruan (Neural Network), pemrograman matlab, Pemrosesan Data, Perencanaan Perkotaan, Perencanaan Sumber Daya, prediksi jumlah penduduk, Radial Basis Function (RBF-NN), sistem prediksi. Bookmark the permalink. 2 Comments.
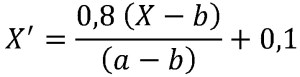







































load net_keluaranload data_prediksi_rbfload hasil_prediksi_rbf
data_prediksi = data_prediksi_rbf(:,12);Error using loadUnable to read file ‘data_prediksi_rbf’. No such file or directory.
File source code lengkap bisa dibeli di tokopedia sehingga tidak muncul error ketika dirunning