Algoritma genetika (AG) merupakan algoritma pencarian yang didasarkan pada mekanisme seleksi alamiah dan genetika alamiah. Karena didasarkan pada teori-teori dalam ilmu biologi, banyak istilah dan konsep biologi yang digunakan dalam algoritma ini. AG telah banyak diterapkan pada beberapa kasus seperti optimasi, pemrograman otomatis, machine learning, pemodelan ekonomi, pemodelan sistem imunisasi, pemodelan ekologis, serta interaksi antara evolusi dan belajar (Suyanto, 2005).

Berikut ini merupakan contoh penerapan algoritma genetika untuk optimasi kombinasi dalam kasus Travelling Salesman Problem. Optimasi dilakukan untuk mencari jalur/rute terpendek yang menghubungkan antara dua titik lokasi. Langkah-langkah pemrogramannya adalah sebagai berikut:

1. Mempersiapkan dan menampilkan data koordinat dari beberapa titik lokasi

clc; clear; close all;

load DataKoordinat

% menampilkan plot masing2 titik
figure,
plot(XY(:,1),XY(:,2),'b.','MarkerSize',20)
grid on
text(XY(1,1),XY(1,2),'  P01')
text(XY(2,1),XY(2,2),'  P02')
text(XY(3,1),XY(3,2),'  P03')
text(XY(4,1),XY(4,2),'  P04')
text(XY(5,1),XY(5,2),'  P05')
text(XY(6,1),XY(6,2),'  P06')
text(XY(7,1),XY(7,2),'  P07')
text(XY(8,1),XY(8,2),'  P08')
text(XY(9,1),XY(9,2),'  P09')
text(XY(10,1),XY(10,2),'  P10')
text(XY(11,1),XY(11,2),'  P11')

tampilan plot koordinat dari beberapa titik lokasi ditunjukkan pada gambar berikut

2. Melakukan pencarian jalur/rute terpendek yang menghubungkan antara dua titik lokasi

JumGen      = length(XY(:,1));         % Jumlah gen
UkPop       = 10;                      % Jumlah kromosom dalam populasi
Psilang     = 0.8;                     % Probabilitas pindah silang
Pmutasi     = 0.005;                   % Probabilitas mutasi
MaxG        = 100;                     % Jumlah generasi

PanjJalHarp = 20;                      % Panjang Jalur yang diharapkan
Fthreshold  = 1/PanjJalHarp;           % Threshold untuk fitness
Bgraf       = Fthreshold;              % Untuk menangani tampilan grafis

hfig = figure;
hold on
set(hfig, 'DoubleBuffer', 'on');
axis([1 MaxG 0 Bgraf]);
hbestplot1 = plot(1:MaxG,zeros(1,MaxG),'r','LineWidth',2);
hbestplot2 = plot(1:MaxG,zeros(1,MaxG),'b','LineWidth',2);
htext1 = text(0.6*MaxG,0.25*Bgraf,sprintf('Fitness terbaik: %7.6f', 0.0));
htext2 = text(0.6*MaxG,0.20*Bgraf,sprintf('Fitness rata-rata: %7.6f', 0.0));
htext3 = text(0.6*MaxG,0.15*Bgraf,sprintf('Panjang jalur terbaik: %7.3f', 0.0));
htext4 = text(0.6*MaxG,0.10*Bgraf,sprintf('Ukuran populasi: %3.0f', 0.0));
htext5 = text(0.6*MaxG,0.05*Bgraf,sprintf('Probabilitas Mutasi: %4.3f', 0.0));
xlabel('Generasi');
ylabel('Fitness');
hold off
drawnow;

% Inisialisasi Populasi
Populasi = TSPInisialisasiPopulasi(UkPop,JumGen);
save Populasi Populasi
for generasi=1:MaxG,
MaxF = TSPEvaluasiIndividu(Populasi(1,:),JumGen,XY);
MinF = MaxF;
IndeksIndividuTerbaik = 1;
for ii=1:UkPop,
Fitness(ii) = TSPEvaluasiIndividu(Populasi(ii,:),JumGen,XY);
if (Fitness(ii) > MaxF),
MaxF = Fitness(ii);
IndeksIndividuTerbaik = ii;
JalurTerbaik = Populasi(ii,:);
end
if (Fitness(ii) <= MinF), MinF = Fitness(ii); end end FitnessRataRata = mean(Fitness); plotvector1 = get(hbestplot1,'YData'); plotvector1(generasi) = MaxF; set(hbestplot1,'YData',plotvector1); plotvector2 = get(hbestplot2,'YData'); plotvector2(generasi) = FitnessRataRata; set(hbestplot2,'YData',plotvector2); set(htext1,'String',sprintf('Fitness terbaik: %7.6f', MaxF)); set(htext2,'String',sprintf('Fitness rata-rata: %7.6f', FitnessRataRata)); set(htext3,'String',sprintf('Panjang jalur terbaik: %7.3f', 1/MaxF)); set(htext4,'String',sprintf('Ukuran populasi: %3.0f', UkPop)); set(htext5,'String',sprintf('Probabilitas Mutasi: %4.3f', Pmutasi)); drawnow if MaxF < Fthreshold,
break;
end

TempPopulasi = Populasi;

% Elitisme:
% - Buat satu kopi kromosom terbaik jika ukuran populasi ganjil
% - Buat dua kopi kromosom terbaik jika ukuran populasi genap
if mod(UkPop,2)==0,           % ukuran populasi genap
IterasiMulai = 3;
TempPopulasi(1,:) = Populasi(IndeksIndividuTerbaik,:);
TempPopulasi(2,:) = Populasi(IndeksIndividuTerbaik,:);
else                          % ukuran populasi ganjil
IterasiMulai = 2;
TempPopulasi(1,:) = Populasi(IndeksIndividuTerbaik,:);
end

LinearFitness = LinearFitnessRanking(UkPop,Fitness,MaxF,MinF);

% Roulette-wheel selection dan pindah silang
for jj=IterasiMulai:2:UkPop,
IP1 = RouletteWheel(UkPop,LinearFitness);
IP2 = RouletteWheel(UkPop,LinearFitness);
if (rand < Psilang),
Anak = TSPPindahSilang(Populasi(IP1,:),Populasi(IP2,:),JumGen);
TempPopulasi(jj,:) = Anak(1,:);
TempPopulasi(jj+1,:) = Anak(2,:);
else
TempPopulasi(jj,:) = Populasi(IP1,:);
TempPopulasi(jj+1,:) = Populasi(IP2,:);
end
end

% Mutasi dilakukan pada semua kromosom
for kk=IterasiMulai:UkPop,
TempPopulasi(kk,:) = TSPMutasi(TempPopulasi(kk,:),JumGen,Pmutasi);
end

Populasi = TempPopulasi;

end

% Tanpa tanda ';' berarti menampilkan nilai dari variabel 'JalurTerbaik'
JalurTerbaik;

% Simpan variabel 'JalurTerbaik' ke dalam file JalurTerbaik.mat
save JalurTerbaik.mat JalurTerbaik

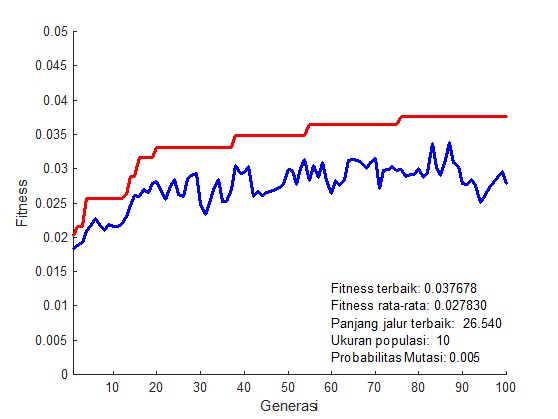
Grafik nilai fitness pada masing-masing generasi ditunjukkan pada gambar berikut

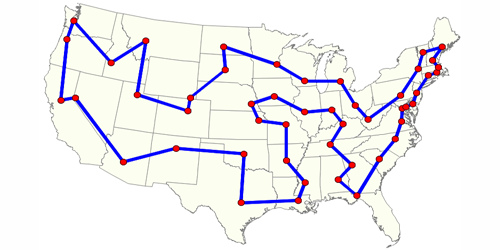
3. Menampilkan hasil pencarian jalur/rute terpendek

% menampilkan plot masing2 titik beserta jalur terbaik
figure,
plot([XY(JalurTerbaik(1),1);XY(JalurTerbaik(2),1)],...
[XY(JalurTerbaik(1),2);XY(JalurTerbaik(2),2)],'r-','LineWidth',2)
hold on
plot([XY(JalurTerbaik(2),1);XY(JalurTerbaik(3),1)],...
[XY(JalurTerbaik(2),2);XY(JalurTerbaik(3),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(3),1);XY(JalurTerbaik(4),1)],...
[XY(JalurTerbaik(3),2);XY(JalurTerbaik(4),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(4),1);XY(JalurTerbaik(5),1)],...
[XY(JalurTerbaik(4),2);XY(JalurTerbaik(5),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(5),1);XY(JalurTerbaik(6),1)],...
[XY(JalurTerbaik(5),2);XY(JalurTerbaik(6),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(6),1);XY(JalurTerbaik(7),1)],...
[XY(JalurTerbaik(6),2);XY(JalurTerbaik(7),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(7),1);XY(JalurTerbaik(8),1)],...
[XY(JalurTerbaik(7),2);XY(JalurTerbaik(8),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(8),1);XY(JalurTerbaik(9),1)],...
[XY(JalurTerbaik(8),2);XY(JalurTerbaik(9),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(9),1);XY(JalurTerbaik(10),1)],...
[XY(JalurTerbaik(9),2);XY(JalurTerbaik(10),2)],'r-','LineWidth',2)
plot([XY(JalurTerbaik(10),1);XY(JalurTerbaik(11),1)],...
[XY(JalurTerbaik(10),2);XY(JalurTerbaik(11),2)],'r-','LineWidth',2)
plot(XY(:,1),XY(:,2),'b.','MarkerSize',20)
text(XY(1,1),XY(1,2),'  P01')
text(XY(2,1),XY(2,2),'  P02')
text(XY(3,1),XY(3,2),'  P03')
text(XY(4,1),XY(4,2),'  P04')
text(XY(5,1),XY(5,2),'  P05')
text(XY(6,1),XY(6,2),'  P06')
text(XY(7,1),XY(7,2),'  P07')
text(XY(8,1),XY(8,2),'  P08')
text(XY(9,1),XY(9,2),'  P09')
text(XY(10,1),XY(10,2),'  P10')
text(XY(11,1),XY(11,2),'  P11')
hold off
grid on

tampilan hasil pencarian jalur/rute terpendek ditunjukkan pada gambar berikut

Source code lengkap dan data pada pemrograman di atas dapat diperoleh melalui halaman berikut ini: Source Code