Travelling Salesman Problem (TSP) adalah salah satu masalah optimasi kombinatorial yang paling terkenal dalam ilmu komputer dan matematika. Dalam masalah ini, seorang salesman harus mengunjungi sejumlah kota yang berbeda tepat satu kali dan kembali ke kota asalnya, sambil mencari rute terpendek yang meminimalkan jarak perjalanan total. Dalam artikel ini, akan dijelaskan bagaimana Algoritma Genetika dapat digunakan untuk menyelesaikan TSP.

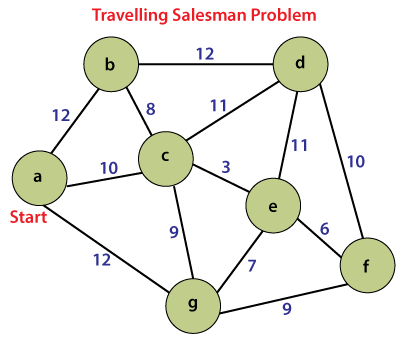
Apa itu Algoritma Genetika?

Algoritma Genetika (AG) adalah teknik optimasi yang terinspirasi dari konsep evolusi dalam biologi. Teknik ini bekerja dengan menghasilkan populasi solusi potensial, menilai kualitasnya, dan kemudian menggunakan operator genetika seperti seleksi, crossover, dan mutasi untuk menghasilkan generasi solusi baru yang lebih baik. AG adalah algoritma heuristik yang dapat digunakan untuk menyelesaikan masalah optimasi kompleks, termasuk TSP.

Langkah-langkah Algoritma Genetika untuk TSP

Berikut adalah langkah-langkah umum dalam menerapkan Algoritma Genetika untuk menyelesaikan TSP:

1. Representasi Kromosom

Setiap individu dalam populasi AG direpresentasikan sebagai kromosom, yang pada dasarnya adalah daftar urutan kota yang akan dikunjungi oleh salesman. Misalnya, jika terdapat 5 kota, kromosom dapat terlihat seperti ini: [1, 3, 2, 5, 4], yang berarti salesman akan mengunjungi kota 1, kemudian kota 3, dan seterusnya.

2. Inisialisasi Populasi

Populasi awal terdiri dari sejumlah individu (kromosom) yang dibuat secara acak atau dengan metode inisialisasi tertentu. Semakin besar populasi, semakin besar variasi yang mungkin dalam pencarian solusi.

3. Evaluasi Fitness

Setiap individu dalam populasi dievaluasi berdasarkan panjang jalur yang ditempuhnya. Dalam TSP, ini berarti menghitung total jarak perjalanan. Tujuan adalah untuk meminimalkan nilai ini.

4. Seleksi

Individu-individu yang memiliki nilai fitness (jarak perjalanan) yang lebih rendah lebih mungkin dipilih sebagai “orangtua” untuk menghasilkan generasi berikutnya. Seleksi dapat dilakukan dengan berbagai metode, seperti Roulette Wheel Selection atau Turnamen.

5. Crossover

Operator crossover digunakan untuk menggabungkan informasi dari dua orangtua yang dipilih dalam populasi. Ini menciptakan keturunan yang memiliki campuran dari keduanya. Dalam TSP, crossover dapat berarti menciptakan solusi baru dengan menggabungkan dua rute yang berbeda.

6. Mutasi

Mutasi adalah operasi acak yang mengubah beberapa elemen dalam kromosom individu. Ini membantu mencegah konvergensi prematur dan meningkatkan variasi dalam populasi.

7. Evaluasi Generasi Baru

Setelah proses seleksi, crossover, dan mutasi selesai, populasi generasi baru dievaluasi kembali untuk menilai kualitasnya.

8. Iterasi

Langkah-langkah 4 hingga 7 diulang sejumlah iterasi atau generasi tertentu atau hingga kondisi berhenti yang ditentukan tercapai.

9. Solusi Terbaik

Solusi terbaik yang ditemukan selama iterasi adalah hasil akhir dari algoritma dan merupakan jawaban perkiraan untuk TSP.

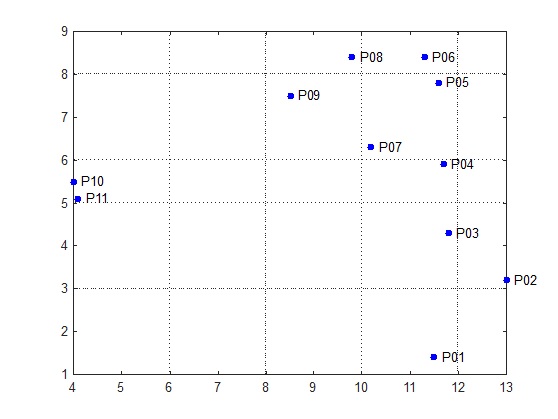
Berikut ini pemrograman MATLAB untuk menyelesaikan Travelling Salesman Problem (TSP) dengan input berupa koordinat antar kota:

% Koordinat antar kota
coordinates = [
    0, 0;
    2, 4;
    5, 2;
    6, 6;
    8, 3;
];

% Menghitung matriks jarak antar kota
numCities = size(coordinates, 1);
distanceMatrix = zeros(numCities, numCities);
for i = 1:numCities
    for j = 1:numCities
        if i ~= j
            distanceMatrix(i, j) = norm(coordinates(i, 🙂 - coordinates(j, :));
        end
    end
end

% Parameter Algoritma Genetika
populationSize = 50;
numGenerations = 100;
mutationRate = 0.02;

% Inisialisasi populasi awal secara acak
population = zeros(populationSize, numCities);
for i = 1:populationSize
    population(i, 🙂 = randperm(numCities);
end

% Evaluasi fitness populasi awal
fitness = zeros(populationSize, 1);
for i = 1:populationSize
    route = population(i, :);
    totalDistance = 0;
    for j = 1:numCities-1
        totalDistance = totalDistance + distanceMatrix(route(j), route(j+1));
    end
    totalDistance = totalDistance + distanceMatrix(route(end), route(1)); % Kembali ke kota awal
    fitness(i) = 1 / totalDistance; % Menentukan fitness sebagai invers dari total jarak
end

% Algoritma Genetika
for generation = 1:numGenerations
    % Seleksi (Roulette Wheel Selection)
    selectedIndices = randsample(1:populationSize, populationSize, true, fitness);
    selectedPopulation = population(selectedIndices, :);

    % Crossover (Partially Mapped Crossover)
    newPopulation = zeros(populationSize, numCities);
    for i = 1:2:populationSize
        parent1 = selectedPopulation(i, :);
        parent2 = selectedPopulation(i+1, :);
        crossoverPoint1 = randi([1, numCities-1]);
        crossoverPoint2 = randi([crossoverPoint1+1, numCities]);

        % Crossover menggunakan Partially Mapped Crossover (PMX)
        child1 = parent1;
        child2 = parent2;
        child1(crossoverPoint1:crossoverPoint2) = parent2(crossoverPoint1:crossoverPoint2);
        child2(crossoverPoint1:crossoverPoint2) = parent1(crossoverPoint1:crossoverPoint2);

        newPopulation(i, 🙂 = child1;
        newPopulation(i+1, 🙂 = child2;
    end

    % Mutasi
    for i = 1:populationSize
        if rand() < mutationRate
            swapIndices = randperm(numCities, 2);
            newPopulation(i, swapIndices) = newPopulation(i, fliplr(swapIndices));
        end
    end

    % Evaluasi fitness populasi baru
    newFitness = zeros(populationSize, 1);
    for i = 1:populationSize
        route = newPopulation(i, :);
        totalDistance = 0;
        for j = 1:numCities-1
            totalDistance = totalDistance + distanceMatrix(route(j), route(j+1));
        end
        totalDistance = totalDistance + distanceMatrix(route(end), route(1));
        newFitness(i) = 1 / totalDistance;
    end

    % Pemilihan generasi berikutnya
    population = newPopulation;
    fitness = newFitness;
end

% Menemukan solusi terbaik dari populasi akhir
bestRouteIndex = find(fitness == max(fitness));
bestRoute = population(bestRouteIndex, :);

% Menampilkan hasil
disp('Solusi Terbaik:');
disp(bestRoute);

Algoritma Genetika adalah teknik yang dapat digunakan dalam menyelesaikan masalah Travelling Salesman Problem. Dengan menggunakan representasi kromosom, operasi genetika, dan evaluasi fitness, AG dapat secara efektif mencari solusi yang mendekati optimal untuk TSP, meskipun masalah ini termasuk dalam kategori masalah NP-hard (Non-deterministic Polynomial time). Algoritma Genetika juga dapat diadaptasi untuk menyelesaikan berbagai masalah optimasi kombinatorial lainnya, menjadikannya alat yang serbaguna dalam bidang ilmu komputer dan matematika.

Source code beserta data lengkap pemrograman MATLAB di atas dapat diperoleh melalui halaman berikut ini: Source Code